Extended Kalman Filter for State Estimation of an Omni-wheel Vehicle
03 Nov 2014This was an assignment for the Autonomous Mobile Robotics (ME597) course I’m taking. Given the vehicle shown below, I needed to come up with a motion model and then use simulated multi-rate GPS data to estimate the state of the vehicle as it executed various paths.
The reason that the extended version of the Kalman Filter was used is that the wheel speeds affect the position of the vehicle in the intertial reference frame in different ways depending on the heading. Thus, the motion update equations are linearized about the current belief of the vehicle’s heading.
Low accuracy GPS data (standard deviation of 0.5 meters North and East) was received at 10 Hz, with more accurate measurements (standard deviation of 0.01 meters North and East) occuring at a rate of 1 Hz. A magnetometer with a standard deviation of of 10 degrees was used to provide information about the vehicle’s heading.
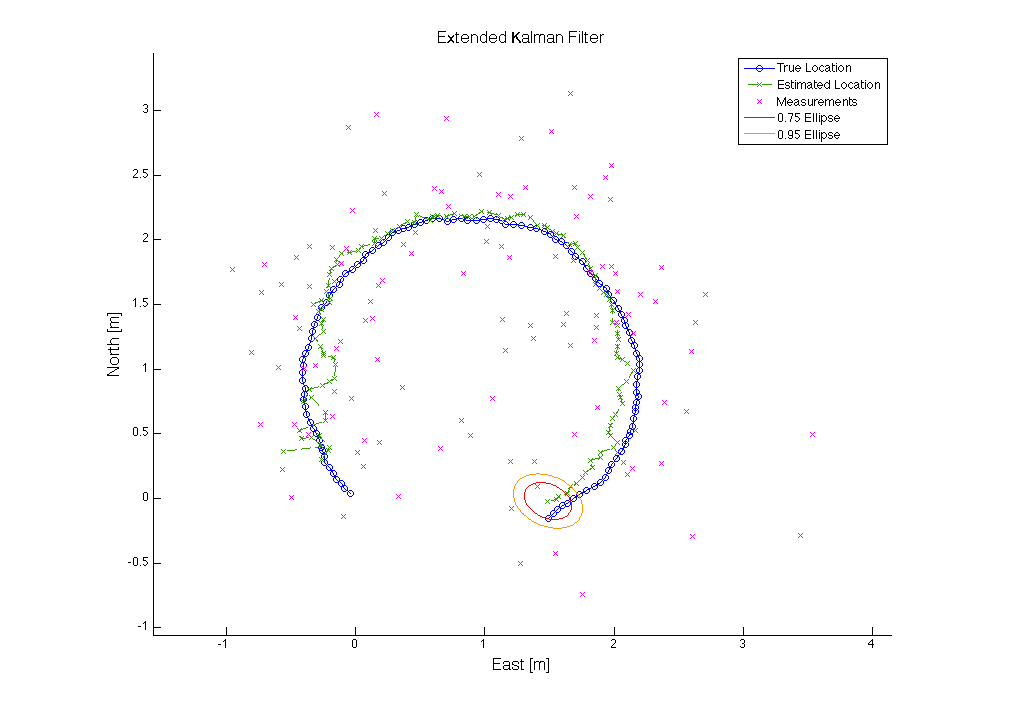
The following figure shows the actual vehicle path in blue, the estimated path in green, with measurements in magenta, using only the low accuracy GPS measurements for state estimation.
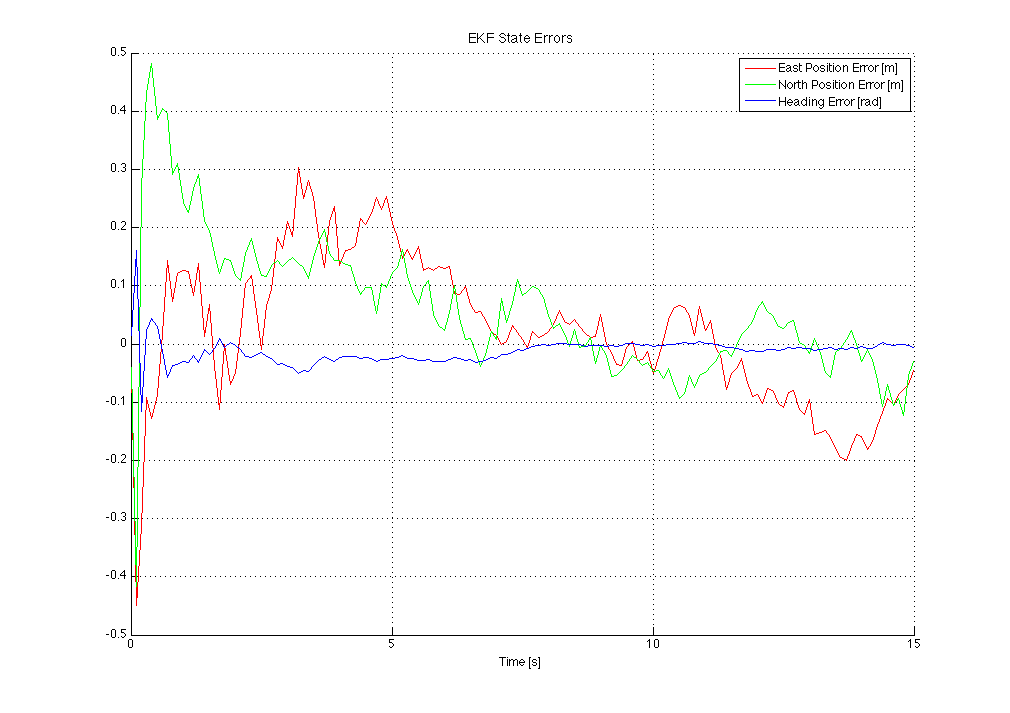
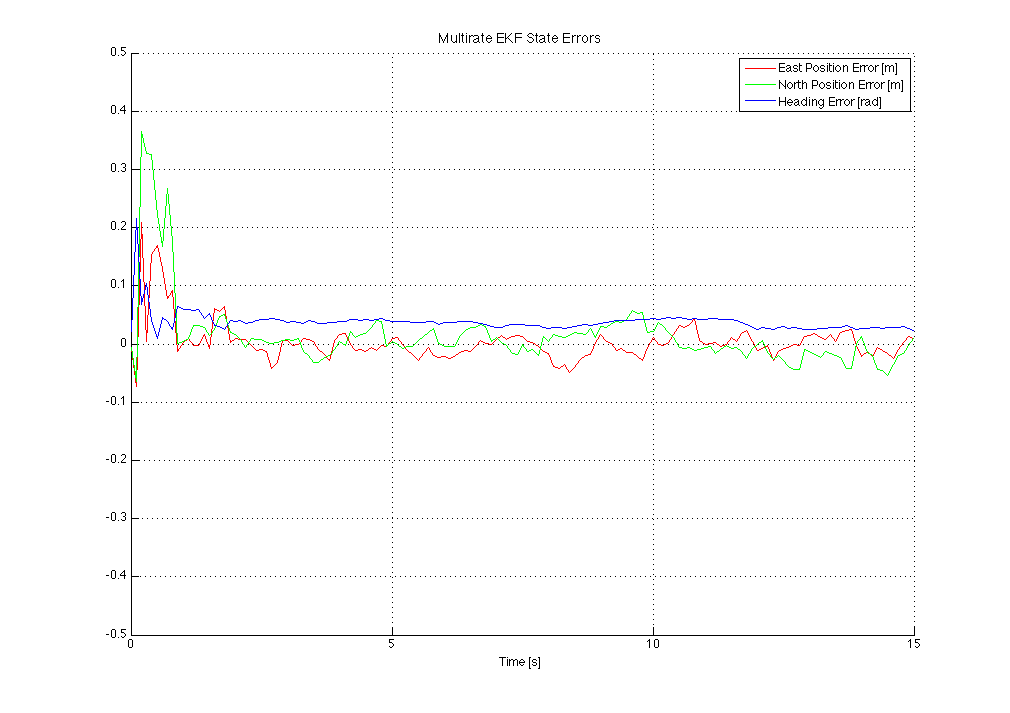
The errors on the each of the state variables are shown below.
This figure also shows the actual vehicle path in blue, the estimated path in green, with measurements in magenta, but uses the multi-rate GPS data for state estimation.
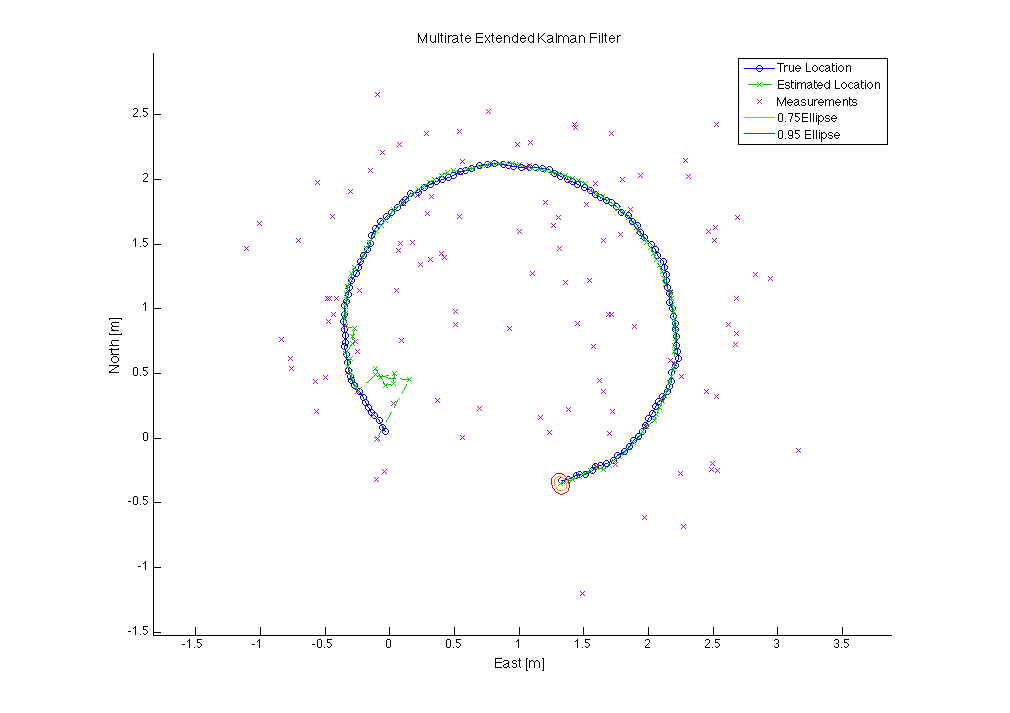
It can be observed that the errors are much lower when the multi-rate GPS data is used.
An additional requirement for the assignment was to come up with an inverse model in order to generate a variety of paths. The vehicle can only be controlled by adjusting the rotational speed of each of the three wheels, which is why the problem is not as trivial as simply specifying the desired velocity in the intertial coordinate frame.
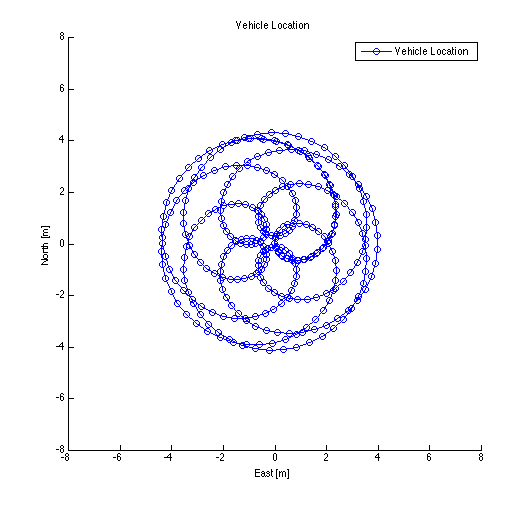
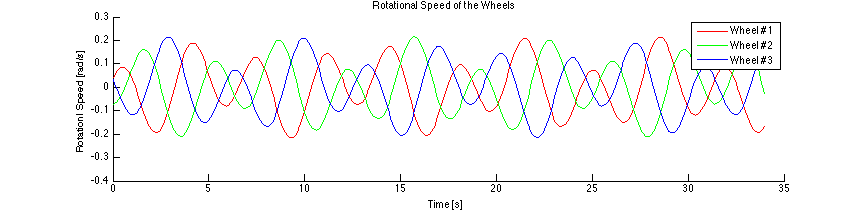
Here is one of the paths generated in this way - an epicycloid. The wheel rotational speeds which produce the path are shown below.
This is definitely one of the most challenging courses I’ve ever taken, but it also ranks as one of the most interesting. The potential impact autonomous vehicles will have is of a magnitude only comparable to nanotechnology and artificial intelligence, so the possibility of playing a role in their development is an extremely exciting prospect for me.
